The web-server can generate two kinds of pseudo k-tuple nucleotide composition (PseKNC) to represent DNA sequences, i.e., Type 1 and Type 2 PseKNC. They are defined as follows.
Type 1 pseudo k-tuple nucleotide composition
Suppose a DNA sequence X with L nucleotides:
X = R1R2R3R4R5R6R7 . . . RL
where R1 represents the nucleotide at position 1, R2 the nucleotide at position 2, and so forth. Therefore, R1R2…Rk is the first corresponding oligonucleotide of length k, R2R3…Rk+1 the second corresponding oligonucleotide of length k, and so forth.
Type 1 pseudo k-tuple nucleotide composition is called the parallel-correlation type and generates 4k+λ discrete numbers to represent a DNA sequence according to PseAAC proposed by Chou [1].
The sequence order effect of R1R2R3R4R5R6R7 . . . RL can be approximately reflected with a set of sequence order-correlated factors as defined below:
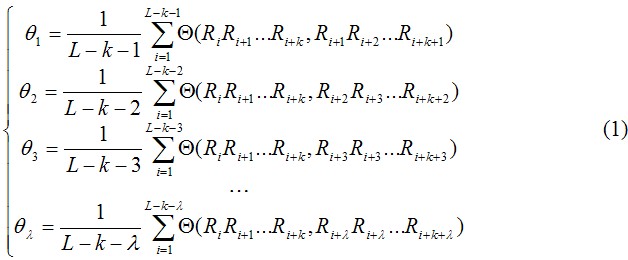
where θ1 is called the first-tier correlation factor that reflects the sequence order correlation between all the most contiguous oligonucleotide of length k along a DNA fragment (Fig. 1a), θ2 the second-tier correlation factor that reflects the sequence order correlation between all the second most contiguous oligonucleotide of length k (Fig.1b), θ3 the third-tier correlation factor that reflects the sequence order correlation between all the 3rd most contiguous oligonucleotide of length k (Fig.1c), and so forth. λ represents the counted rank (or tier) of the correlation along a DNA sequence and is smaller than L-k. Generally, the greater the λ, the more order information included in the PseKNC, however, the too large λ means redundant information and may lead to poorer prediction performance and longer training time.
In Eq. 2 the correlation function is given by
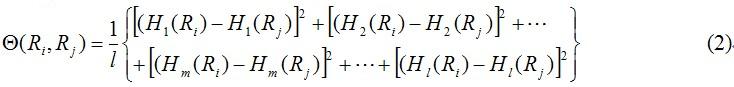
where Hm(Ri) (m=1, 2, 3, …, l; m is the number of physicochemical property of the oligonucleotide of length k) is the physicochemical property of the oligonucleotide RiRi+1Ri+2…Ri+k and Hm(Rj) the corresponding value for the oligonucleotide RjRj+1Rj+2…Rj+k. Note that before substituting the values of physicochemical property into Eq.2, they were all subjected to a standard conversion as described by the following equation:
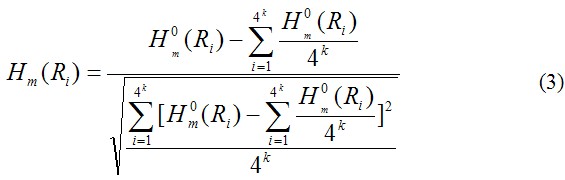
where
is the original physicochemical property value of the ith oligonucleotide of length k (i=1, 2, …, 4k) that can be obtained from corresoponing references [2-28]. Without loss of generality, we use the numerical indices 1, 2, 3, …, 4k to represent the 4k native oligonucleotide of length k. The advantage to use the converted physicochemical property values obtained via Eq. 3 is that they will have a zero mean value over the 4k native oligonucleotide of length k and will remain unchanged if going through the same conversion procedure again.
As we can see from Figure 1, the sequence order effect of a DNA can be, to some extent, reflected through a set of sequence-correlation factors θ1, θ2, θ3, …, θλ, as defined by Eq. 1. Now let us augment the formulation of nucleic composition to include such a set of discrete numbers. To realize this, instead of using a 4k-D (dimensional) vector defined by 4k components, we use a (4k+λ)-D vector defined by 4k+λ discrete numbers to represent a DNA X; i.e.,
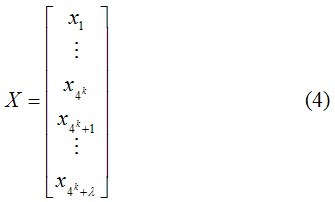
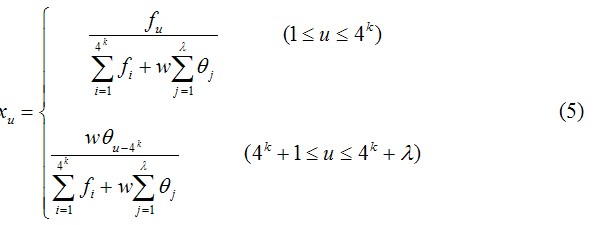
where fi is the normalized occurrence frequency of the 4k oligonucleotides of length k in the DNA sequence X, θj is the j-tier sequence correlation factor computed according to Eqs. 1-3 for DNA sequence X, and w is the weight factor for the sequence order effect.
As we can see from Eqs. 4 and 5, the first 4k components reflect the effect of the nucleic acid composition, whereas the components from 4k+1 to 4k+λ reflect the effect of sequence order. A set of such 4k+λ components as formulated by Eqs. 4 and 5 is called the Type 1 PseKNC for DNA sequence X.
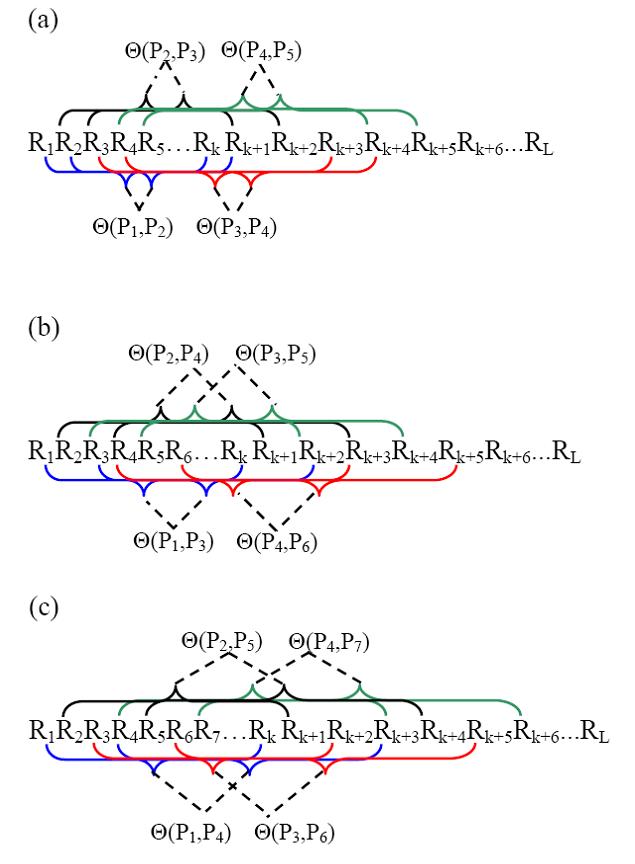
Figure 1. A schematic drawing to show (a) the first-tier, (b) the second-tier, and (c) the third-tier sequence order correlation mode along a DNA fragment. Panel (a) reflects the correlation mode between all the most contiguous oligonucleotide of length k, panel (b) that between all the secon-most contiguous oligonucleotide of length k, and panel (c) that between all the third-most contiguous oligonucleotide of length k. P1 indicates the first corresponding oligonucleotide of length k R1R2…Rk, P2 the second oligonucleotide of length k R2R3…Rk+1, and so forth.
Type 2 pseudo k-tuple nucleotide composition
Type 2 pseudo k-tuple nucleotide composition (PseKNC) is called the series-correlation type PseKNC and generates 4k+l*λ discrete numbers to represent a DNA sequence (l is the number of physicochemical property attributes selected). Type 2 PseKNC was defined according to PseAAC proposed by Chou in 2005 [29].
The basic idea of Type 2 PseKNC is as following:
The physicochemical properties of the oligonucleotide of length k were used to formulate the sequence-order correlated factors in the following equations.
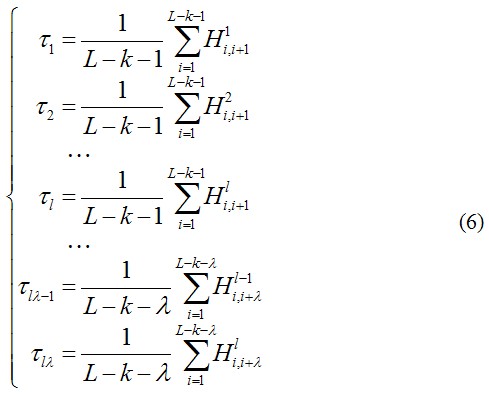
where
, 
, … and 
are corresponding physicochemical correlation functions of the l physicochemical properties corresponding to each oligonucleotide of length k (Fig. 2) and can be given by
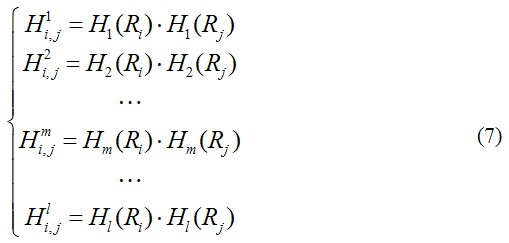
where Hm(Ri) (m=1, 2, 3, …, l; m is the number of physicochemical property of the oligonucleotide of length k) is the physicochemical property of the oligonucleotide RiRi+1Ri+2…Ri+k and Hm(Rj) the corresponding value for the oligonucleotide RjRj+1Rj+2…Rj+k. The dot (●) means the multiplication sign. Note that before substituting the values of physicochemical property into Eq.7, they were all subjected to a standard conversion as described by the following equation:
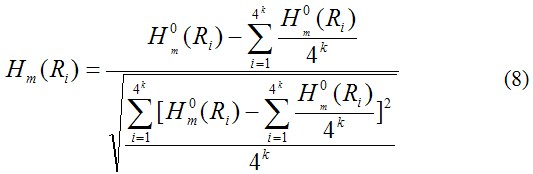
where
is the original physicochemical property value of the ith oligonucleotide of length k (i=1, 2, …, 4k) that can be obtained from corresoponing references [2-28]. Without loss of generality, we use the numerical indices 1, 2, 3, …, 4k to represent the 4k native oligonucleotide of length k. The advantage to use the converted physicochemical property values obtained via Eq. 8 is that they will have a zero mean value over the 4k native oligonucleotide of length k and will remain unchanged if going through the same conversion procedure again.
After incorporating the sequence-order correlated factors from Eq. 7 into the classical 4k-D (dimensional) nucleic acid composition, we obtain a PseKNC with (4k+ l*λ) components. In other words, the representation for a DNA sequence X is now formulated as:
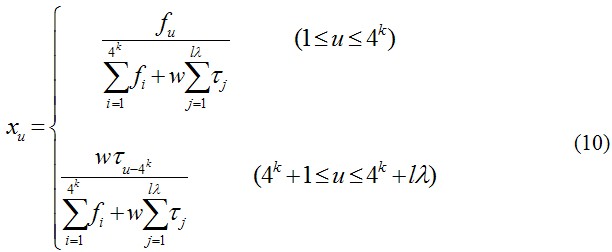
where fi is the normalized occurrence frequency of the 4k oligonucleotides of length k in the DNA sequence X, j is the j-tier sequence correlation factor computed according to Eq. 1 for the DNA sequence X.
As we can see from Eqs. 9 and 10, the first 4k components reflect the effect of the nucleic acid composition, whereas the components from 4k+1 to 4k+l*λ reflect the physicochemical sequence-order pattern. A set of such 4k+l*λ components is called Type 2 PseKNC or the physicochemical PseKNC.
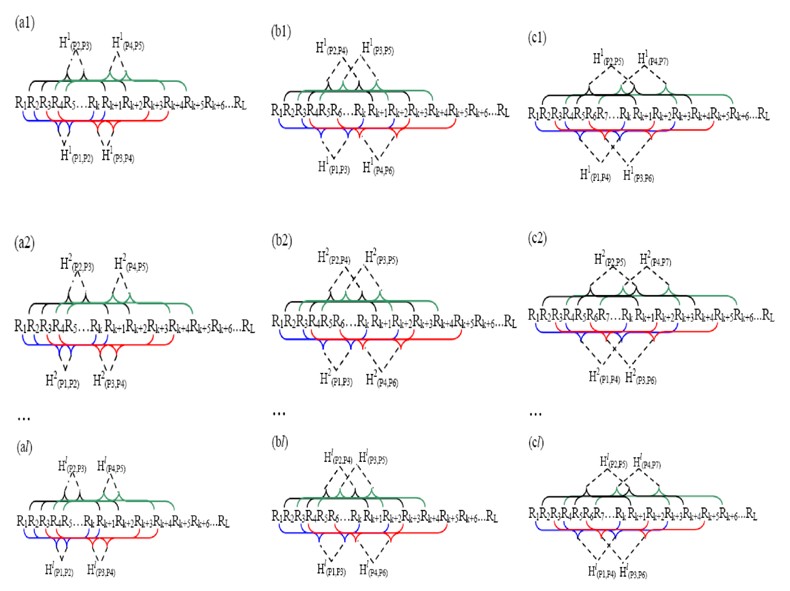
Figure 2. A schematic drawing to show (a1…al) the first-tier, (b1…bl) the second-tier, and (c1…cl) the third-tier sequence-order-coupling mode along a DNA sequence through l physicochemical property correlation functions, where, ，…, andare given by Equation (3). Panel (a1…al) reflects the correlation mode between all the most contiguous oligonucleotide of length k, panel (b1…bl) that between all the secon-most contiguous oligonucleotide of length k, and panel (c1…cl) that between all the third-most contiguous oligonucleotide of length k. P1 indicates the first corresponding oligonucleotide of length k R1R2…Rk, P2 the second oligonucleotide of length k R2R3…Rk+1, and so forth.
1. Chou KC: Prediction of protein cellular attributes using pseudo-amino acid composition. Proteins 2001, 43(3):246-255.
2. Brukner I, Sanchez R, Suck D, Pongor S: Sequence-dependent bending propensity of DNA as revealed by DNase I: parameters for trinucleotides. EMBO J 1995, 14(8):1812-1818.
3. Vlahovicek K, Kajan L, Pongor S: DNA analysis servers: plot.it, bend.it, model.it and IS. Nucleic Acids Res 2003, 31(13):3686-3687.
4. Ulyanov NB, James TL: Statistical analysis of DNA duplex structural features. Methods Enzymol 1995, 261:90-120.
5. Sugimoto N, Nakano S, Yoneyama M, Honda K: Improved thermodynamic parameters and helix initiation factor to predict stability of DNA duplexes. Nucleic Acids Res 1996, 24(22):4501-4505.
6. Sivolob AV, Khrapunov SN: Translational positioning of nucleosomes on DNA: the role of sequence-dependent isotropic DNA bending stiffness. J Mol Biol 1995, 247(5):918-931.
7. Sarai A, Mazur J, Nussinov R, Jernigan RL: Sequence dependence of DNA conformational flexibility. Biochemistry 1989, 28(19):7842-7849.
8. SantaLucia J, Jr., Allawi HT, Seneviratne PA: Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry 1996, 35(11):3555-3562.
9. Olson WK, Gorin AA, Lu XJ, Hock LM, Zhurkin VB: DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proc Natl Acad Sci U S A 1998, 95(19):11163-11168.
10. Lisser S, Margalit H: Determination of common structural features in Escherichia coli promoters by computer analysis. Eur J Biochem 1994, 223(3):823-830.
11. Lewis JP, Sankey OF: Geometry and energetics of DNA basepairs and triplets from first principles quantum molecular relaxations. Biophys J 1995, 69(3):1068-1076.
12. Ivanov VI, Minchenkova LE, Chernov BK, McPhie P, Ryu S, Garges S, Barber AM, Zhurkin VB, Adhya S: CRP-DNA complexes: inducing the A-like form in the binding sites with an extended central spacer. J Mol Biol 1995, 245(3):228-240.
13. Ho PS, Ellison MJ, Quigley GJ, Rich A: A computer aided thermodynamic approach for predicting the formation of Z-DNA in naturally occurring sequences. EMBO J 1986, 5(10):2737-2744.
14. Hartmann B, Malfoy B, Lavery R: Theoretical prediction of base sequence effects in DNA. Experimental reactivity of Z-DNA and B-Z transition enthalpies. J Mol Biol 1989, 207(2):433-444.
15. Gromiha MM, Ponnuswamy PK: Hydrophobic distribution and spatial arrangement of amino acid residues in membrane proteins. Int J Pept Protein Res 1996, 48(5):452-460.
16. Gorin AA, Zhurkin VB, Olson WK: B-DNA twisting correlates with base-pair morphology. J Mol Biol 1995, 247(1):34-48.
17. el Hassan MA, Calladine CR: Propeller-twisting of base-pairs and the conformational mobility of dinucleotide steps in DNA. J Mol Biol 1996, 259(1):95-103.
18. Aida M: An ab initio molecular orbital study on the sequence-dependency of DNA conformation: an evaluation of intra- and inter-strand stacking interaction energy. J Theor Biol 1988, 130(3):327-335.
19. Breslauer KJ, Frank R, Blocker H, Marky LA: Predicting DNA duplex stability from the base sequence. Proc Natl Acad Sci U S A 1986, 83(11):3746-3750.
20. Ornstein RL, Rein R, Breen DL, Macelroy RD: An optimized potential function for the calculation of nucleic acid interaction energies. Biopolymers 1978, 17(10):2341-2360.
21. Chalikian TV, Volker J, Plum GE, Breslauer KJ: A more unified picture for the thermodynamics of nucleic acid duplex melting: a characterization by calorimetric and volumetric techniques. Proc Natl Acad Sci U S A 1999, 96(14):7853-7858.
22. Gotoh O TY: Stabilities of nearest neighbour doublets in double helical DNA determined by fitting calculated melting profiles to observed profiles. Biopolymers 1980, 20(5):1033-1042.
23. Satchwell SC, Drew HR, Travers AA: Sequence periodicities in chicken nucleosome core DNA. J Mol Biol 1986, 191(4):659-675.
24. Goodsell DS, Dickerson RE: Bending and curvature calculations in B-DNA. Nucleic Acids Res 1994, 22(24):5497-5503.
25. Ivanov VI KD, Shchyolkina AK, Chernov BK, Minchenkov LE.: Decimal code controlling the B to A transition of DNA. J Biomol Struct Dynamics 1995, 12:105-108.
26. Blake R: Encyclopedia of molecular biology and molecular medicine. New York: Wiley; 1996.
27. Munteanu MG, Vlahovicek K, Parthasarathy S, Simon I, Pongor S: Rod models of DNA: sequence-dependent anisotropic elastic modelling of local bending phenomena. Trends Biochem Sci 1998, 23(9):341-347.
28. Goni JR, Perez A, Torrents D, Orozco M: Determining promoter location based on DNA structure first-principles calculations. Genome Biol 2007, 8(12):R263.
29. Chou KC: Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics 2005, 21(1):10-19.